Enigmes du musicien
Ces trois énigmes deviennent accessibles via le menu Extras une fois les différences trouvées sur les 9 photos de l'album photo (voir section Appareil photo).
Enigme 139 : Côte est, côte ouest (70 picarats)
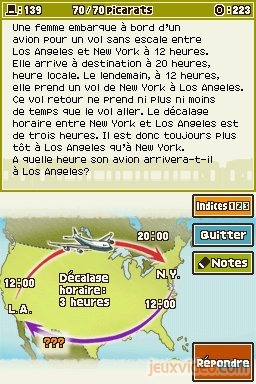
Une femme fait un trajet aller-retour en avion de Los Angeles à New York. Il y a 3 heures de décalage horaire entre les deux villes, New York étant en avance sur Los Angeles. A l'aller, la femme est partie à midi et est arrivée à 20 heures, heure locale. Si elle n'avait pas avancé sa montre de 3 heures, elle serait arrivée à 17h (17 + 3). Donc le trajet aller a duré 5 heures. Si le vol retour ne met pas plus de temps, il faudra 5 heures pour revenir à Los Angeles. En partant à midi, elle arrivera donc à 17h, soit 14h heure locale (17 - 3). Réponse : 14.

Enigme 140 : Pour un cube de plus (70 picarats)
Un gros cube est constitué de 28 petits cubes. Il a été formé en emboîtant 5 pièces les unes dans les autres. Il faut trouver à quelle pièce appartient le petit cube qui dépasse du cube final. L'avantage, c'est qu'on sait que les pièces ne doivent pas être tournées. Il faut donc imaginer comment les pièces peuvent s'emboîter les unes dans les autres par simple translation. On peut déjà éliminer la pièce D, car le cube qui dépasserait ne se trouverait pas au centre de l'ensemble. C doit également être éliminé car il ne permettrait plus à D de s'insérer dans le cube. Il faut donc commencer à placer C et D, puis à réfléchir comment emboîter les trois pièces restantes correctement. Il apparaît que le cube qui dépasse de l'ensemble appartient finalement à B. Réponse : B.


Enigme 141 : Sauts de billes 6 (99 picarats)
La solution de ce sixième plateau de billes est donnée sur cette vidéo.
Enigmes de l'herboriste
Ces trois énigmes deviennent accessibles via le menu Extras une fois que vous avez servi le thé à 26 personnes (voir section Service à Thé).
Enigme 142 : Une vie (60 picarats)
Il faut deviner combien a duré l'existence d'un mathématicien en se basant sur ses dires qu'on peut transformer en équation. La valeur x correspond au temps de vie du mathématicien.
"J'ai passé 1/6 de ma vie à l'état d'enfant, 1/12 de ma vie en tant que jeune homme, puis 1/7 de ma vie plus tard je me suis marié" :
x/6 + x/12 + x/7
"Après 5 ans de mariage, j'ai eu la chance d'avoir un enfant qui n'a malheureusement vécu que la moitié du temps où j'ai été en vie avant de mourir. Aujourd'hui, 4 ans après son décès, c'est à mon tour de quitter ce monde" :
5 + x/2 + 4
L'équation donne : x = x (1/6 + 1/12 + 1/7 + 1/2) + 5 + 4
Avec un dénominateur commun : x = x (14/84 + 7/84 + 12/84 + 42/84) + 9
x = x (75/84) + 9 = 75x/84 + 9
x - 75x/84 = 9
84x/84 - 75x/84 = 9
9x/84 = 9
x/84 = 1
x = 84
Le mathématicien est mort à 84 ans.


Enigme 143 : Chiffres et lettres (60 picarats)
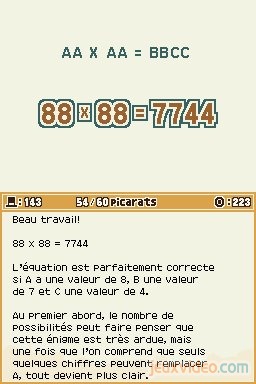
On transforme une multiplication de chiffres (11 x 11 = 121) par une multiplication de lettres (AA x AA = ABA), où A = 1 et B = 2. Suivant ce principe, il faut trouver quelles valeurs correspondent à A, B et C dans : AA x AA = BBCC.
Il n'y a qu'à tester chaque résultat pour toutes les valeurs possibles de A :
11 x 11 = 121
22 x 22 = 484
33 x 33 = 1089
44 x 44 = 1936
55 x 55 = 3025
66 x 66 = 4356
77 x 77 = 5929
88 x 88 = 7744 = BBCC si B = 7 et C = 4
99 x 99 = 9801
La seule réponse possible est donc : A = 8, B = 7 et C = 4.


Enigme 144 : Piles de crêpes 4 (99 picarats)
Déplacez les crêpes de la manière suivante :
Enigmes du cuisinier
Ces trois énigmes deviennent accessibles via le menu Extras une fois l'entraînement du hamster terminé (voir section Hamster).
Enigme 145 : 500 perles (70 picarats)
La mission d'un voyageur est de pénétrer dans une grotte contenant 500 perles pour en ramener un certain nombre. Ce nombre doit permettre de diviser les perles en lots de 2, 3, 4, 5, 6 ou 7 perles, tout en laissant toujours une perle de côté. Combien a-t-il ramené de perles, sachant que ce nombre (x) ne permet pas d'obtenir des lots de 4 perles tout en en laissant une de côté ? Pour résumer, il faut que x - 1 soit divisible par 2, 3, 5, 6 et 7, mais pas par 4. On trouve : x - 1 = 210.
En effet :
210 / 2 = 105
210 / 3 = 70
210 / 4 = 52,5
210 / 5 = 42
210 / 6 = 35
210 / 7 = 30
Si x - 1 = 210, alors x = 211. Le voyageur a donc ramené 211 perles.


Enigme 146 : Boîte à angles (70 picarats)
Il nous faut trouver la mesure d'un angle obtenu en plaçant trois points A, B et C au centre de trois arêtes d'un cube. Aucun calcul n'est nécessaire ici. En effet, si on continuait à tracer les arêtes de cette façon, on finirait par obtenir un hexagone régulier. Et comme il s'agit d'une figure dont les angles saillants font 120°, la réponse est 120.


Enigme 147 : Labyrinthe secret (80 picarats)
Les morceaux d'un labyrinthe ont été mélangés comme dans un taquin. Vous devez les remettre en ordre en déplaçant les pièces, mais encore faut-il bien se représenter le modèle... Le rond-point doit être au centre, le bassin au milieu à droite, la croix au milieu en bas, et le point noir en haut à gauche. Cette vidéo vous donne la solution.
Enigmes des amoureux
Ces trois énigmes deviennent accessibles via le menu Extras une fois l'aventure principale achevée.
Enigme 148 : Huit cartes (70 picarats)
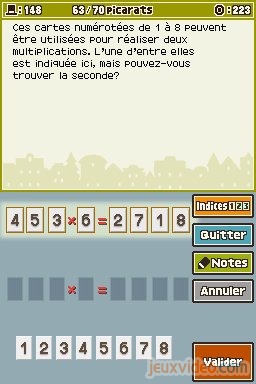
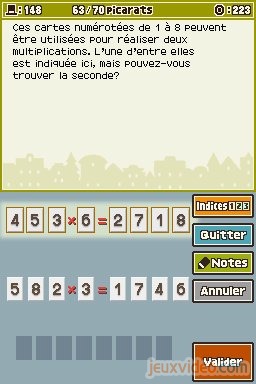
En combinant d'une certaine façon les chiffres de 1 à 8, on peut obtenir deux multiplications différentes. La première nous est donnée : 453 x 6 = 2718. Il faut deviner la seconde. Il n'y a pas d'astuce particulière pour parvenir au résultat. La solution est : 582 x 3 = 1746.

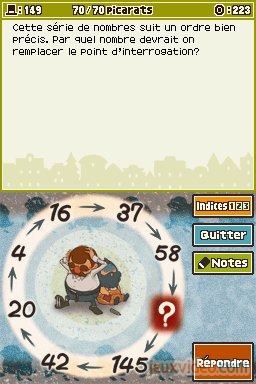
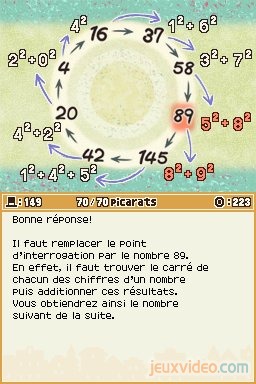
Enigme 149 : A la suite (70 picarats)
Il faut compléter une suite de nombres : 4, 16, 37, 58, ?, 145, 42, 20. En étudiant chaque chiffre indépendamment, on se rend compte que l'opération qui permet de passer d'un nombre à un autre consiste à additionner chaque chiffre qui le compose après les avoir fait passer au carré.
Ainsi : 4² = 16, 1² + 6² = 37, etc.
Le nombre que l'on cherche est : x = 5² + 8², soit 25 + 64 ; x = 89.
Enigme 150 : Cavalier en balade 4 (99 picarats)
Un cavalier se déplace sur un échiquier constitué de 64 cases. L'objectif est de faire en sorte qu'il s'arrête une seule fois sur toutes les cases de l'échiquier. Le bon parcours vous est donné sur cette vidéo.
Enigmes de l'expert
Ces trois dernières énigmes ne se débloquent qu'une fois les 150 énigmes résolues !
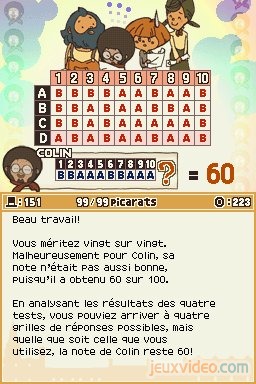
Enigme 151 : La note de Colin (99 picarats)
A partir des notes obtenues par trois élèves à un QCM, vous devez deviner quelle a été la note de Colin. Il faut donc commencer par recouper les réponses de chacun pour trouver quelles étaient les bonnes réponses à chaque question. Le fait que Mary ait obtenu la note de 70/100 signifie qu'elle a donné 7 bonnes réponses sur 10. En se basant sur le fait que Lisa n'a trouvé que 3 bonnes réponses, on peut penser que la majorité des réponses qu'elle a en commun avec les autres sont des réponses justes. On en trouve 4 (aux questions n°1, 3, 7 et 8), mais comme Lisa n'a eu que 30 points, l'une des 4 doit être fausse. Comme vous pouvez le craindre, en poursuivant ce raisonnement, on risque d'arriver à plusieurs configurations possibles pour les réponses justes et fausses. Heureusement, toutes donnent le même résultat ! Colin a obtenu 60 points à son QCM.

Enigme 152 : Partie de cartes (80 picarats)
Patrick participe à un tournoi de cartes dans lequel chacun doit affronter tous les autres en duel. Sachant que 59 parties ont été jouées, on veut savoir au bout de combien de matches Patrick s'est retiré du tournoi. Le nombre de parties jouées dans un tournoi est égal au nombre de joueurs multiplié par le nombre de joueurs moins un, le tout divisé par deux.
P = (J x (J-1))/2
De toute évidence, si Patrick était resté jusqu'au bout, il y aurait eu au minimum 60 parties jouées. Essayons de trouver une valeur pour J (le nombre de joueurs) qui permette d'avoir un P (nombre de parties) supérieur ou égal à 60.
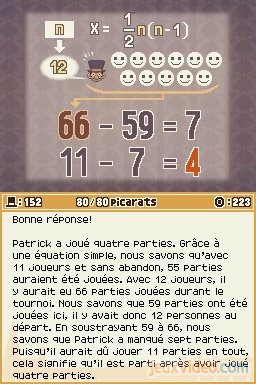
Si J = 12, alors P = (12 x 11)/2 = 132/2 = 66.
Maintenant qu'on a trouvé le nombre de joueurs (12) et de parties qui auraient dues être jouées (66), il n'y a plus qu'à retrancher le nombre de parties qui ont réellement été jouées (59) pour trouver combien de matches Patrick a manqué : 66 - 59 = 7. A 12 participants, il aurait dû affronter 11 adversaires et donc faire 11 duels. S'il en a manqué 7, on en déduit qu'il en a tout de même fait 4. Réponse : 4.
Enigme 153 : Piège final (99 picarats)
L'objectif est de placer la gemme rose dans le cercle en bas de l'écran. Déplacez les blocs comme indiqué sur cette vidéo. Vous pouvez réussir en 78 coups.