Salut, voici l'énoncé : Calcule l'aire de la partie d'un plan comprenant l'origine du plan,délimitée par le cercle de centre O(0;0) et de rayon 3 et la droite comprenant les points A(0;-3) et B(2;sqrt(5))

Alors voilà j'ai fait une représentation graphique du problème sur géogébra 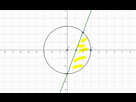la partie en jaune c'est bien l'aire que je dois calculer ?

J'ai subdivisé en calcule de 4 aires comme voici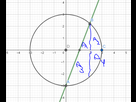

Donc pour A1=l'intégrale de la droite de 1,14 jusque 2

Pour A2= l'intégrale du cercle(sqrt(9-x^2)) de 2 jusque 3

Pour A3=- l'intégrale de la droite de 0 jusque 1,14 (car la fonction est négative sur cet intervalle)

Pour A4= - l'integrale du cercle (-sqrt(9-x^2)) de 2 jusque 3

c'est bien ça pour la résolution ?, j'ai pas fait de fautes ?

Selon moi, tu t'es planté de partie. "Calcule l'aire de la partie du plan comprenant l'origine du plan."
Dans ton cas, la partie jaune ne contient pas l'origine. Donc c'est l'autre bout de cercle qu'il faut calculer.

salut quand on veut calculer l'aire du 3ème quadrant t'es bien d'accord que l'équation du cerce est -sqrt(9-×^2) et lorsqu'on veut calculer l'intégrale entre a et b il faut mettre un - car la fct est négative ?