Je voudrais montrer que In = intégrale de 0 à 1 de (ln(t)^n)/(1-t)dt vaut (-1)^n * n! * zeta(n+1)

J'ai bien une égalité 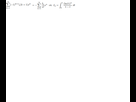et en "identifiant" je trouve le bon In seulement je crois pas que je suis censé devoir utiliser de résultats sur les séries entières

Tu as un résultat classique pour $\mathrm {Re}(s)>1$ :
$$ \Gamma(s)\zeta(s) = \int_0^\infty \frac{u^{s-1}}{\mathrm e^u - 1}\,\mathrm du $$
Si tu fais le changement de variable $t = \mathrm e^{-u}$ tu obtiens :
$$ \Gamma(s)\zeta(s) = \int_0^1 \frac{(-\log t)^{s-1}}{1-t}\,\mathrm dt $$
avec la détermination principale du log. En particulier pour $n$ entier :
$$ (-1)^n\cdot n! \cdot \zeta(n+1) = (-1)^n\cdot \Gamma(n+1)\zeta(n+1) = \int_0^1 \frac{(\log t)^{n}}{1-t}\,\mathrm dt $$